De ware ernst van de huidige coronacrisis is moeilijk in te zien. Uit alle richtingen wordt er met cijfers gestrooid, cijfers die soms met elkaar in tegenspraak lijken te zijn, en bovendien onderschattingen zijn. Hoeveel mensen zijn inmiddels besmet geraakt, welk deel daarvan is ziek geworden en welk deel is helaas overleden? Die vragen probeer ik te beantwoorden aan de hand van een model.
In een eerder artikel beweerde ik dat het aantal mensen dat in Nederland besmet is met het coronavirus vele malen hoger is dan het aantal mensen bij wie het virus ook daadwerkelijk is vastgesteld. Hetzelfde geldt, in mindere mate, voor het werkelijke aantal coronaslachtoffers. Dit komt vooral doordat in Nederland overlijdensgevallen aan het coronavirus toeschrijven als dat onomstotelijk is vastgesteld. In België worden twijfelgevallen wel meegenomen, waardoor ze veel meer coronaslachtoffers hebben. Het aantal gerapporteerde coronadoden loopt bij onze zuiderburen echter veel beter in de pas met de zogenaamde oversterfte.
Het lijkt erop dat beide Lage Landen ongeveer even zwaar zijn getroffen door het coronavirus. Waar in België de infectiegraad onder bloeddonoren eind maart ongeveer 2 procent was en twee weken later 4 procent, was het percentage in Nederland begin april ongeveer 3 procent. De tijdsperiodes zijn te vaag en te globaal om een analyse aan op te hangen, vooral ook omdat het niet goed bekend is hoelang iemand geïnfecteerd moet zijn met het coronavirus voordat hij of zij een te detecteren hoeveelheid antilichamen aanmaakt. Wat echter wel mogelijk is, is om een model te maken waarin het verloop van de coronacrisis zo nauwkeurig mogelijk gemodelleerd wordt.
In een eerder model gebruikte ik het aantal coronaslachtoffers om het werkelijke aantal besmettingen terug te rekenen. Een complicatie bij een model waarin je het verleden probeert te voorspellen is dat het toevoegen van een incubatietijd een statistisch bezwaar heeft. Daarom probeer ik ditmaal voor België (dat betrouwbaardere cijfers heeft) het aantal coronaslachtoffers te schatten aan de hand van het aantal werkelijke besmettingen. Schematisch werkt het model als volgt:
Gerapporteerde besmettingen –>
Werkelijke besmettingen –>
Werkelijke slachtoffers
Het aantal werkelijke besmettingen Z op dag t is hierbij gemodelleerd als 1/f maal het aantal gerapporteerde besmettingen N i dagen later, waarbij i de incubatietijd is en f de kans dat iemand die besmet is ook op de ziekte getest wordt (grof gezegd de kans dat ‘ie ook daadwerkelijk ziek wordt). Z kan vervolgens worden vergeleken met de infectiegraad onder bloeddonoren. Een complicerende factor hierbij is dat iemand die het virus heeft opgelopen niet meteen antistoffen in zijn of haar bloed heeft. Dat proces schijnt best lang te kunnen duren. Dit betekent dat dat de werkelijke incubatietijd (veel) groter is dan de waargenomen incubatietijd, zoals hieronder schematisch is weergegeven.
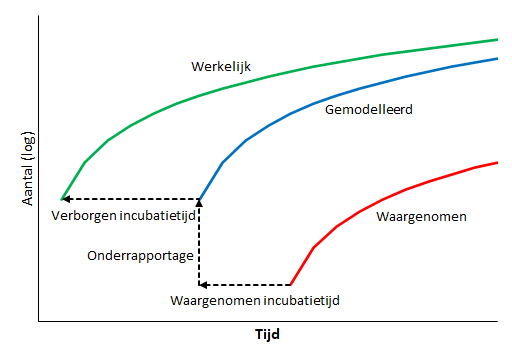
Het (hypothetische) verloop van het werkelijke aantal besmettingen is dus gelijk aan die van het gemodelleerde verloop, maar dan een aantal dagen eerder, aangenomen dat de incubatietijd voor iedereen hetzelfde is. Het betekent dat de tijd tussen besmetting en overlijden wordt onderschat, wat geen onoverkomelijk probleem is, omdat deze tijd later nog in het model geschat gaat worden. De kans dat een willekeurig iemand overlijdt is p en de tijd d die het duurt voordat dat gebeurt is normaal verdeeld, d ~ N(μ,σ).
Het model bepaalt nu voor elke dag hoeveel mensen er daadwerkelijk besmet zijn (Z), gebaseerd op het aantal waargenomen besmettingen, een nader te bepalen incubatietijd i en de kans dat een besmet persoon ook ziek wordt (f).
Allereerst moeten de parameters van het aantal werkelijke besmettingen worden gekalibreerd aan de hand van de infectiegraden onder bloeddonoren. Deze infectiegraden heb ik vastgeprikt op 24 maart en 7 april (twee weken later), wat misschien wat conservatieve schattingen zijn, die wellicht een deel van de verborgen incubatietijd opnemen. Het blijkt dat een incubatietijd i van 5 dagen en een een kans om ziek te worden f van 4% goed aansluit bij de infectiegraden van bloeddonoren.
Vervolgens kunnen de parameters voor de overlijdenskans geschat worden. Het aantal mensen dat op dag j zal overlijden, is de som van het aantal mensen dat in de dagen ervoor besmet is geraakt (de afgeleide van Z, ofwel z), vermenigvuldigd met de kans dat ze op dag j zullen overlijden. Aan de hand hiervan kunnen p, μ en σ bepaald worden. Een overlijdenskans p van 1,5%, een μ van 20 en een σ van 5 dagen blijkt erg goed op de data aan te sluiten, zoals hieronder te zien is.
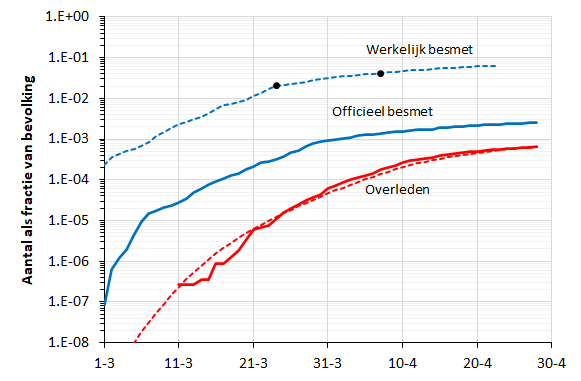
De parameters suggereren dus dat:
– Momenteel ruim 6% van de bevolking besmet is
– 4% van de mensen die besmet is ook ziek wordt
– 3 op de 8 mensen die ziek worden ook overlijden
– 1½% van de besmette mensen overlijden
– 95% daarvan tussen de 10 en 30 dagen na de besmetting overlijdt (en dat is exclusief de verborgen incubatietijd)
De cijfers gelden natuurlijk voor België, maar afgaande op de infectiegraden onder bloeddonoren verwacht ik dat het in Nederland niet anders zal zijn. In België is inmiddels 0,7 promille van de bevolking aan corona overleden. Dat is echt serieus als je bedenkt dat jaarlijks ongeveer een procent van de bevolking overlijdt. En dan is de coronacrisis nog (lang) niet voorbij.