Dit jaar staan er grote reglementswijzigingen op stapel in de Formule 1, wijzigingen die de rangorde volledig door elkaar kunnen gooien. Het afgelopen jaar werd echter nog gedomineerd door het team van McLaren, dat beide kampioenschappen won, maar ook zij hadden betere en mindere optredens. Lag dat aan het circuit of aan de coureurs? Met behulp van een statistische analyse hoop ik antwoord op te geven.
Halverwege het seizoen keek Max Verstappen tegen een gigantische achterstand aan in het kampioenschap, maar in het najaar ging hij helemaal los, terwijl McLaren inzakte. “Onze auto komt op dit circuit niet goed uit de verf”, of woorden van gelijke strekking gaven Zak Brown en de zijnen dan nogal schouderophalend als verklaring voor de mindere prestaties, maar was dat ook zo?
Sporters kunnen goede en slechte dagen hebben en Formule 1-coureurs vormen daar geen uitzondering op. Anders dan bij de meeste andere sporten zit er in de Formule 1 ook verschil in uitrusting, de ene coureur rijdt nou eenmaal in een betere auto dan de andere. De auto’s hebben allemaal net andere karakteristieken en zijn voor sommige circuits beter geschikt dan voor andere. Is het mogelijk om deze verstorende invloed weg te filteren?
Ja, tot op zekere hoogte kan dit, omdat ieder team twee coureurs heeft. In de onderstaande figuur heb ik de snelste ronde van Lando Norris en Oscar Piastri per raceweekend uitgezet tegen de gemiddelde snelste ronde van de coureurs van de vier topteams (McLaren, Mercedes, Red Bull en Ferrari) als redelijk stabiel referentieniveau. Hierdoor is goed te zien in welke races de McLaren-coureurs relatief sterk of zwak waren.
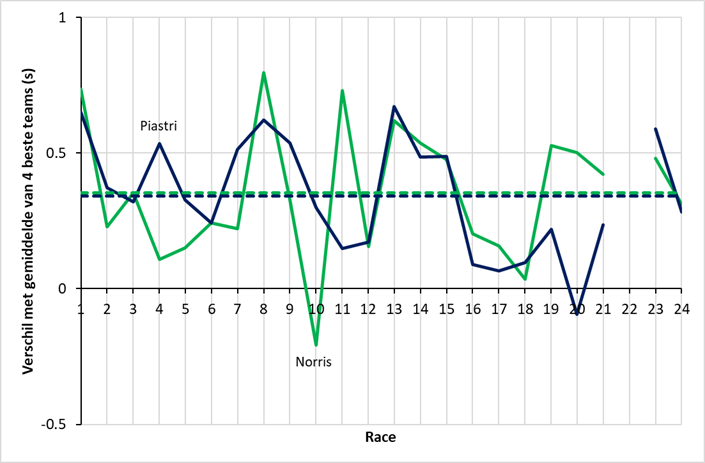
Gemiddeld was Norris een fractie sneller dan Piastri (0,35 om 0,34 seconde sneller dan de gemiddelde coureur van de vier topteams, zie de stippellijnen). De pieken in de eerste race (Australië), alsmede die in race 8 (Monaco) en de zwakkere optredens tegen het eind van het seizoen vallen op. Daarnaast valt Norris’ zwakke optreden in race 10 (Canada), gevolgd door zijn sterke optreden in Oostenrijk op. Piastri was alleen in race 20 (Mexico) trager dan de gemiddelde coureur van de vier topteams. De resultaten van het weekend in Las Vegas (race 22) heb ik vanwege de regen buiten beschouwing gelaten.
Norris’ vorm in de kwalificatie was wat volatieler dan die van Piastri, met een standaarddeviatie van 0,25 seconde om 0,21 seconde. Hierin zit dus ook wat volatiliteit doordat de McLaren op het ene circuit beter uit de verf kwam dan op het andere. Om deze ruis uit de data te halen, vergelijk ik per weekend de snelste rondetijd van Norris met die van Piastri. Doordat ze met dezelfde auto rijden, maakt het niet uit dat het ene circuit de auto beter ligt dan het andere. De standaarddeviatie van het verschil in snelste rondetijd per weekend is 0,26 seconde. Liever gebruik ik in het vervolg overigens de variantie, het kwadraat van de standaarddeviatie, want dat maakt de berekeningen er een stuk eenvoudiger op.
Aangenomen dat de volatiliteit van de prestaties van de coureurs en de auto niet van elkaar afhangen, kan de onderliggende variantie van de coureurs en de auto als volgt worden bepaald:
- c1 + m = N
- c2 + m = P
- c1 + c2 = V
Waarbij:
c1 – Onderliggende variantie Norris
c2 – Onderliggende variantie Piastri
m – Onderliggende variantie McLaren
N – Waargenomen variantie Norris
P – Waargenomen variantie Piastri
V – Waargenomen variantie Norris – Piastri
Invullen voor N, P en V geeft:
- c1 + m = 0.061 ( = 0.25²)
- c2 + m = 0.045 ( = 0.21²)
- c1 + c2 = 0.069 ( = 0.26²)
Dit levert het volgende plaatje op, waarbij de variantie van Piastri (c2) is uitgezet tegen die van Norris (c1). Vergelijking (3) is in het oranje weergegeven. Door vergelijking (1) en (2) met elkaar te combineren kan de zwarte lijn worden geconstrueerd. Het snijpunt van de twee lijnen geeft de gezochte waarden van c1 en c2.
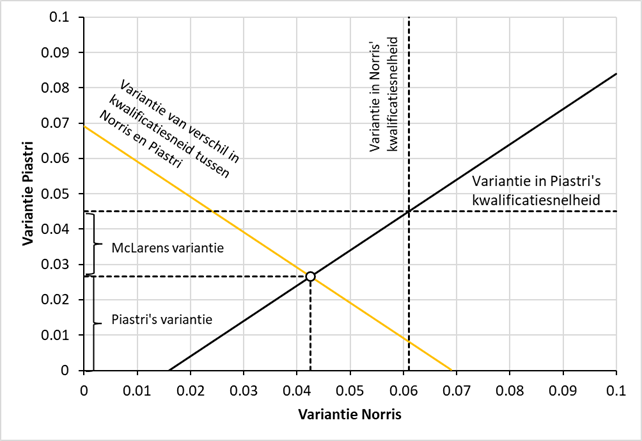
Het blijkt dat de onderliggende variantie van Norris (c1) 0.043 is, die van Piastri (c2) 0.027 en die van McLaren (m) 0.018. Oplossen voor m kan ook door de eerste twee vergelijkingen bij elkaar op te tellen en de derde vergelijking ervan af te trekken. Hieruit volgt:
m = (N + P – V)/2
m = (0.061 + 0.045 – 0.069)/2 = 0.018
Omrekenen naar standaarddeviaties krijg je een standaarddeviatie van 0.21 voor Norris, 0.16 voor Piastri en 0.14 voor McLaren. Norris is dus volatieler dan Piastri en allebei zijn ze iets volatieler dan de auto.
De laatste stap is om voor ieder kwalificatieresultaat een decompositie te maken van de inbreng van de coureur en die van het team. Het volgende plaatje schetst de situatie:
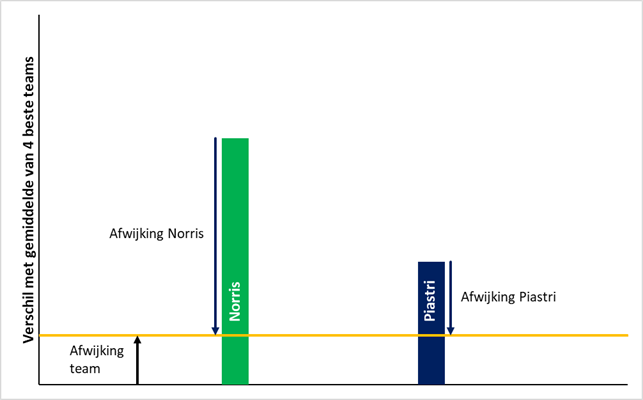
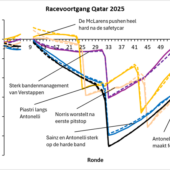
Te zien zijn de fictieve prestaties van Norris (groene balk) en Piastri (donkerblauwe balk) in een race, afgezet tegen het gemiddelde van de coureurs van de vier beste teams. Te zien is dat beide coureurs een goede sessie hebben afgewerkt. Een deel hiervan wordt verklaard door de auto (de oranje lijn) en een deel door de coureurs, die boven verwachting goed reden. De meest waarschijnlijke decompositie van de inbreng van het team en de coureurs minimaliseert de (voor standaarddeviatie gewogen) lengte van de pijlen. De onderstaande figuur geeft de meest waarschijnlijke decompositie per race:
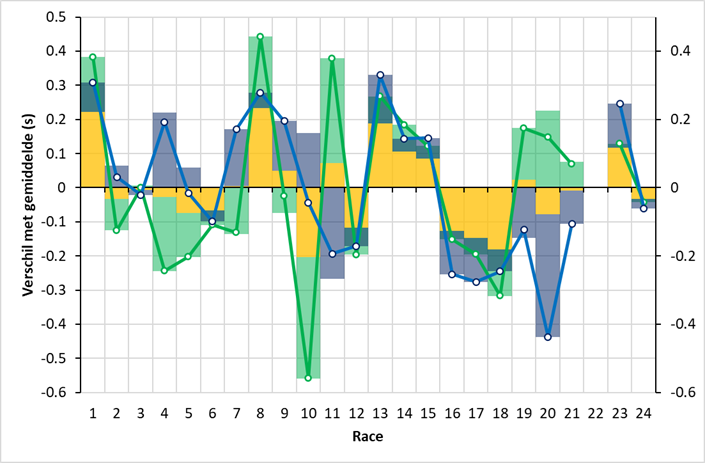
Te zien is dat McLaren (oranje balken) met name in Australië (race 1) als Monaco (race 8) een erg goede auto had. Rond de zomerstop (België t/m Nederland, race 13-15) zijn ze eveneens sterk, maar daarna komen drie races waarin ze dat niet zijn (Italië t/m Singapore). Canada (race 10) is eveneens een slechte race voor McLaren, omdat Norris daar een zwakke kwalificatie reed. Omgekeerd is Piastri’s derde tijd volgens de analyse een puike prestatie. In Oostenrijk (race 11) was Norris een halve seconde sneller dan Piastri. Volgens de analyse kwam dit niet echt door de auto en was Norris’ optreden erg goed, terwijl Piastri een van zijn mindere optredens kende. Opvallend is verder Piastri’s vormverlies vanaf Italië (race 16). Norris heeft ook een dipje, maar hij herstelt zich in race 19 (Amerika), waar Piastri blijft kwakkelen.
Voor de andere coureurs is eenzelfde analyse te maken. Voor de vier topteams zijn de berekende standaarddeviaties per coureur als volgt:
Russell (Mercedes) 0.12
Leclerc (Ferrari) 0.13
Verstappen (Red Bull) 0.16
Piastri (McLaren) 0.16
Norris (McLaren) 0.21
Hamilton (Ferrari) 0.26
Antonelli (Mercedes) 0.27
Lawson/Tsunoda (Red Bull) 0.30
En voor de teams:
Red Bull 0.11
McLaren 0.14
Ferrari 0.19
Mercedes 0.23
Interessant was Russell dus de meest constante coureur volgens de analyse. Inderdaad was de Brit het toonbeeld van consistentie, getuige zijn negen podiumplaatsen, in tegenstelling tot het team. Waarschijnlijk heeft het fiasco in Monaco daarmee te maken, waar beide coureurs zich om verschillende redenen in de staart van de middenmoot kwalificeerden. Ook Leclerc kende een constant seizoen en was zelfs nog wat constanter dan Verstappen en Piastri. Omgekeerd waren Hamilton, Antonelli of de tweede Red Bull-coureur behoorlijk inconsistent. Opmerkelijk genoeg komt Red Bull bij de teams uit de bus als het meest constante team, ondanks de matige optredens in Oostenrijk en Hongarije halverwege het seizoen.
De standaarddeviaties van de teams liggen in de buurt van die van de consistentere coureurs. Voor hen is een slechte kwalificatie in principe even vaak de schuld van de auto als van zijzelf. Voor de minder consistente coureurs geldt dat niet. Als zij een slechte kwalificatie hebben, ligt dat vaker aan henzelf. McLaren had een auto die redelijk allround was en had daarnaast redelijk constante coureurs, wat de vraag oproept wat er in het najaar toch in hemelsnaam gebeurd is met Piastri, die zes zwakke optredens op rij had.
