De rol van de technologie
In het vorige deel van deze serie heb ik uiteengezet waarom er in de Formule 1 doorgaans maar weinig inhaalacties plaatsvinden: de combinatie van bochtige circuits en auto’s die de rijwind gebruiken om neerwaartse kracht op te wekken is daarvoor buitengewoon ongeschikt. Inderdaad was het aantal inhaalacties in veel races in de jaren 90 tot aan het DRS-tijdperk op de vingers van een hand te tellen.
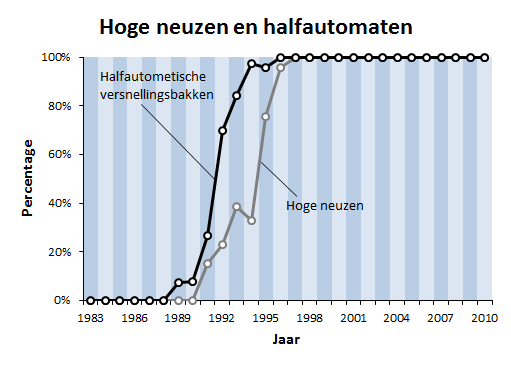
De invloed van de aerodynamica neemt af op het moment dat de auto’s moeilijker te besturen zijn en de coureurs dus meer fouten maken. De technologie speelt daarbij een grote rol. Zo werden de stalen remschijven in de jaren 80 al langzaam maar zeker vervangen door koolstof remschijven, die betere en vooral consistentere prestaties leveren. Een andere ontwikkeling was de overgang van de handgeschakelde versnellingsbak naar de halfautomatische versnellingsbak in het begin van de jaren 90, waardoor het schakelen een stuk sneller en makkelijker ging (coureurs konden niet meer per ongeluk een verkeerde versnelling inschakelen met alle gevolgen van dien). Inderdaad is de afname van het aantal inhaalacties vaak afgeschoven op de komst van de halfautomatische versnellingsbak.
Ook op aerodynamisch gebied werden er in die tijd grote stappen gemaakt. Zo had Tyrrell in 1990 als eerste een auto met een hoge neus. Het idee achter het concept was dat er meer lucht onder de auto naar de diffuser geleid kon worden, wat een hoop extra neerwaartse kracht opleverde zonder dat het ten koste ging van veel extra luchtweerstand (hoe lucratief dit is bleek wel in 2012, toen vrijwel alle teams voor een geknakte neus kozen). De vondst werd gauw overgenomen door het team van Benetton, dat de voorvleugel onder de neus liet doorlopen. Zodoende leverde de hoge neus nog een tweede voordeel op: meer vleugeloppervlak omdat de voorvleugel niet meer door de neus werd gescheiden. Een mogelijke bijwerking hiervan was dat de auto ook gevoeliger werd voor de vuile lucht in het zog van zijn voorganger. Interessant genoeg werd de hoge neus pas na een serie ingrijpende reglementsveranderingen in 1995 het dominante ontwerp.
Omgekeerde analyse
Hoewel het in kaart brengen van technologische ontwikkelingen als halfautomatische versnellingsbakken en hoge neuzen relatief eenvoudig is, is het alsnog erg lastig om een causaal effect op de hoeveelheid inhaalacties aan te tonen.
Een betere methode is daarom waarschijnlijk de omgekeerde benadering van het probleem. Het idee is om zo veel mogelijk controlevariabelen te verzamelen die niets met aerodynamica van doen hebben, zodat de intrinsieke moeilijkheid van het inhalen per jaar en per circuit door het model geschat wordt. Het idee is dat de data gebruikt wordt om een perfecte simulator te creëren. Wat gebeurt er bijvoorbeeld met het aantal inhaalacties als een race uit 1985 ineens met auto’s uit 1995 gereden wordt?
In dat opzicht heb ik wel stappen gezet sinds de publicatie van mijn boek, want toen had ik nog niet zoveel controlevariabelen. Laten we eerst een hele simpele race modelleren, eentje zonder pitstops. Het aantal verwachte inhaalacties is dan waarschijnlijk een functie van 1) het aantal auto’s, 2) de betrouwbaarheid van de auto’s en 3) hoezeer de auto’s na de start “uit positie” zijn.
Punt 1 behoeft waarschijnlijk geen toelichting. Meer auto’s betekent meer inhaalacties. De mate waarin dit toeneemt is echter wel een punt van discussie. Neemt het lineair toe, of juist kwadratisch (2 keer zoveel auto’s betekent 4 keer zoveel interacties en dan waarschijnlijk 4 keer zoveel inhaalacties), iets ertussenin of juist iets heel anders? Punt 2 is om dezelfde reden ook nogal voor de hand liggend. Als er meer auto’s in competitie blijven, zal er meer worden ingehaald.
Punt 3 is niet moeilijk te begrijpen, maar wel moeilijk te meten. Doorgaans komen de inhaalacties op naam van coureurs die op een plek rijden waar ze eigenlijk niet horen. Ze zijn dus uit positie. Meestal betreft het een snelle coureur die door pech of eigen onkunde bij de start op achterstand is gezet en dus een stevige inhaalrace voor de boeg heeft (het omgekeerde is ook mogelijk, zie bijvoorbeeld de regenachtige Grand Prix van Europa in 2007). Ik heb een manier bedacht om deze menging in een getal uit te drukken (en die berekening zal ik later uit de doeken doen), zodat ook voor de menging van het veld gecontroleerd kan worden.
Vervolgens voeg ik circuit- en jaar-dummyvariabelen toe. Het aantrekkelijke hiervan is dat de jaardummy’s voor de technologie en aerodynamica controleren, waarvan de invloed lastig op voorhand van te voorspellen is. Het aantal inhaalacties is dus als volgt gemodelleerd:
Aantal inhaalacties = aantal auto’s^α x betrouwbaarheid^β x menging^γ x circuitdummy’s x jaardummy’s
Stel dat de begincondities goed zijn voor een potentieel van 50 inhaalacties. Wanneer inhalen makkelijk is, zal dit potentieel voor het grootste gedeelte worden gerealiseerd. Wanneer het moeilijker is om in te halen, zal alleen het laaghangende fruit worden geplukt en valt het aantal inhaalacties lager uit. In de jaren 90 zou een goed circuit in deze omstandigheden bijvoorbeeld nog maar 30 inhaalacties (60% van het potentieel) opleveren. Op een slecht circuit, zoals Monaco, blijft de oogst misschien beperkt tot maar 5 inhaalacties (10% van het potentieel).
Op deze manier is de invloed van de circuits en de technologie indirect te schatten en daardoor kan er eventueel een verklaring gevonden worden voor de afname van het aantal inhaalacties in de jaren 80 en jaren 90. Dergelijk bewijs is echter nog steeds indirect omdat de data is geaggregeerd op raceniveau. Bovendien zijn er nog andere problemen met de analyse, zoals ik in het volgende deel zal laten zien.