De coronapandemie is als een olietanker die zich moeilijk laat bijsturen en waarvan de koers moeilijk te bepalen is. De gerapporteerde gevallen zijn slechts het topje van de ijsberg en daarnaast lopen deze cijfers altijd achter vanwege de incubatietijd van het virus, waardoor het effect van de lockdown maar moeilijk in te schatten is.
Onlangs vond ik een interessant filmpje op YouTube waarin werd geprobeerd het verloop van het echte aantal besmettingen over de tijd te reconstrueren op basis van het aantal gerapporteerde gevallen. Dit werd gedaan voor de befaamde coronahaarden als Italië, Zuid-Korea en natuurlijk de Chinese provincie Hoebee (Hubei) waar het allemaal begon.
Het idee was om aan de hand van de incubatietijd (de tijd tussen besmetting en de eerste ziektesymptomen) en het aantal gerapporteerde besmettingen het echte aantal besmettingen terug te rekenen. Het echte aantal besmettingen op, laten we zeggen, 21 januari was dan het aantal gerapporteerde besmettingen op 22 januari vermenigvuldigd met de kans dat de incubatietijd één dag was, plus het aantal gerapporteerde besmettingen op 23 januari vermenigvuldigd met de kans dat de incubatietijd twee dagen was, enzovoorts. De incubatietijd werd hierbij verondersteld normaal verdeeld te zijn (met een gemiddelde van 8 dagen en een standaarddeviatie van 3 dagen).
Dankzij dit staaltje reverse engineering kon voor elke dag het echte aantal besmettingen worden uitgerekend. Of niet? De methode heeft namelijk een statistisch bezwaar, wat duidelijk wordt doordat de verdeling van het echte aantal besmettingen een grotere spreiding heeft dan die van het aantal gerapporteerde besmettingen. Dit hoort niet zo te zijn en dat kan ik illustreren aan de hand van een simpel voorbeeld.
Stel dat de helft van de bevolking besmet wordt op 1 maart en de andere helft op 2 maart. Stel nu dat de incubatietijd van de helft van de bevolking 2 dagen is en van de andere helft van de bevolking 3 dagen en dat de incubatietijd onafhankelijk is van de tijd waarop iemand besmet wordt. In dit geval wordt een kwart van de bevolking ziek op 3 maart (degenen die op 1 maart besmet werden en een incubatietijd van 2 dagen hadden), de helft van de bevolking wordt ziek op 4 maart en een kwart op 5 maart (dat waren dus degenen die op 2 maart besmet werden en een incubatietijd van 3 dagen hadden). De spreiding van de incubatietijd zorgt er dus voor dat de spreiding van het aantal gerapporteerde gevallen groter is dan die van het echte aantal.
Waar de in het YouTube-filmpje gebruikte methode spaakloopt is dat de eerste gerapporteerde gevallen niet, zoals impliciet wordt aangenomen, een willekeurige incubatietijd hadden, maar hoogstwaarschijnlijk een korte. Dit betekent dat er een methode gevonden moet worden die de spreiding van de incubatietijd van de spreiding van het aantal gerapporteerde gevallen aftrekt in plaats van optelt.
Dit is mogelijk wanneer je het aantal gerapporteerde gevallen eveneens als een normaal verdeelde grootheid beschouwt. Interessant genoeg blijkt het aantal gerapporteerde nieuwe gevallen in Nederland redelijk goed benaderd te worden door een normale verdeling. In maart was er een sterke stijging, die in april zijn maximum bereikte en de afgelopen weken voorzichtig begon te dalen. De piek lijkt rond 9 april te liggen en de standaarddeviatie bedraagt ongeveer 15 dagen.
Het echte aantal besmettingen is dan eveneens normaal verdeeld, met een gemiddelde dat gelijk is aan 1 april (9 april minus de gemiddelde incubatietijd van 8 dagen) en een standaarddeviatie die iets kleiner is dan de standaarddeviatie van het aantal gerapporteerde nieuwe gevallen, namelijk de wortel van de variantie van het aantal gerapporteerde nieuwe gevallen (15²) minus de variantie van de incubatietijd (3²), ofwel ongeveer 14,7 dagen. Doordat de variantie (het kwadraat van de standaarddeviatie) van de incubatietijd veel lager is dan die van de variantie van het aantal gerapporteerde nieuwe gevallen, is de standaarddeviatie van het echte aantal nieuwe besmettingen nagenoeg gelijk aan die van het aantal gerapporteerde nieuwe besmettingen.
In de onderstaande grafieken staan het (werkelijke) verloop van het aantal gerapporteerde nieuwe besmettingen, het gemodelleerde verloop ervan en het gemodelleerde verloop van het echte aantal besmettingen.
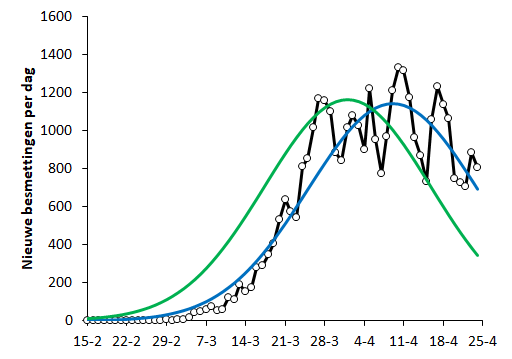

De grafiek van het aantal gerapporteerde nieuwe gevallen is inmiddels over zijn hoogtepunt heen, wat betekent dat het echte aantal nieuwe gevallen nu echt al veel lager is dan rond de piek in begin april. Mocht het model accuraat zijn, dan zitten we nu in het staartje van de crisis.
Interessant genoeg is het effect van de lockdown nog steeds niet goed in de cijfers te ontdekken. Dat komt natuurlijk deels doordat de dag-op-dag-variatie eruit is gefilterd in het model, maar je zou verwachten dat het echte aantal nieuwe besmettingen rond 12 maart zou moeten pieken, wat dus niet het geval is geweest.
Heeft de lockdown dan wel zin gehad? Of werd het effect ervan pas drie weken later zichtbaar? Volgde de pandemie in Nederland wel een exponentiële groeicurve, of zou hij hoe dan ook een cumulatieve normale verdeling hebben gevolgd? Wie het weet mag het zeggen, want zelfs gecorrigeerd voor de incubatietijd is er rond de lockdown geen duidelijke trendbreuk in de cijfers te ontdekken.

