Over anderhalve week begint de KNSB-competitie weer. Een afgeslankt BSG zal zijn eerste competitiewedstrijd in ruim anderhalf jaar tijd tegen De Stukkenjagers spelen. Het is een mogelijk vierpuntenduel in een seizoen waarin BSG toch vooral tegen degradatie zal vechten. Daarom heb ik me weer eens in het spelletje verdiept. Ik heb me gebogen over de vraag waarom de toren in het schaakspel beduidend sterker is dan de loper.
In het schaakspel komt de beweging van de toren en de loper nagenoeg overeen. Het verschil is dat de beweging van de loper met een hoek van 45 graden gedraaid is ten opzichte van de toren. Waar de toren horizontaal en verticaal mag bewegen, beweegt de loper altijd diagonaal. Toch blijkt de toren in de praktijk duidelijk het sterkste stuk. Waar de toren ongeveer 5 pionnen waard is, is de loper er maar 3 waard. Hoe komt dat?
Kijkend naar de mobiliteit van de stukken, dan valt op dat de toren op een leeg schaakbord altijd naar 14 velden kan. In tegenstelling tot alle andere stukken heeft de toren dus geen last van de rand van het bord! De loper wel. In het centrum kan hij naar 13 velden, maar aan de rand slechts naar 7. Hieronder heb ik een heatmap van de loper gemaakt:

De kracht van de loper varieert dus van bijna net zo sterk als de toren tot half zo sterk als de toren. Doordat er meer velden aan de rand zijn dan in het centrum, ligt de gemiddelde mobiliteit van de loper meer in de buurt van het minimum dan van het maximum, namelijk 8,75 velden. De toren is dus gemiddeld 1,6 (14/8,75) keer mobieler dan de loper en dit komt behoorlijk goed overeen met de relatieve waarde van de stukken (5 om 3 punten, ofwel: de toren is 1,67 keer meer waard dan de loper). Het feit dat de loper slechts de helft van de velden kan bereiken, lijkt zijn waarde dus nauwelijks negatief te beïnvloeden.
Dat is interessant, maar hoe zit het op een groter schaakbord? Dan heeft de loper minder last van de rand van het bord en zou het stuk dus sterker moeten worden ten opzichte van de toren. Dat blijkt inderdaad zo te zijn, maar er is een grens. Mathematisch gezien schijnt de toren altijd minimaal anderhalf keer zo mobiel te zijn als de loper. Ik heb dit nagetrokken voor schaakborden tot 100 bij 100 velden en het lijkt inderdaad te kloppen:
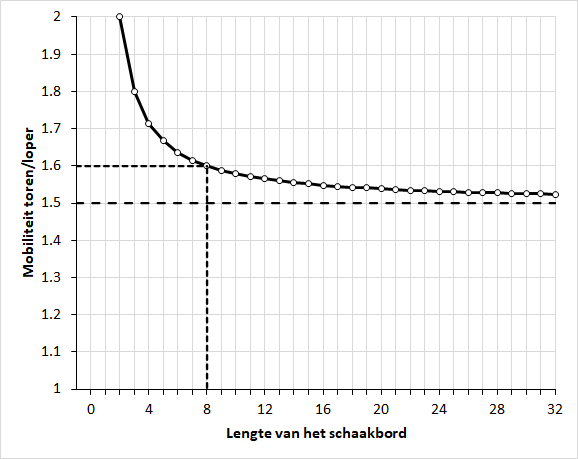
De toren is dus altijd minimaal anderhalf keer zo mobiel (en dus anderhalf keer zo sterk) als de loper. Waarom de toren sterker is? Voor een groot gedeelte door Pythagoras. Diagonalen zijn op het schaakbord nou eenmaal net zo lang als lijnen en rijen, terwijl de werkelijke afstand volgens de stelling van Pythagoras een factor √2 (≈1,41) groter is, waardoor een deel van de kracht van de loper verloren gaat. Dit verklaart voor het grootste gedeelte het verschil in mobiliteit tussen de toren en loper, maar dus niet helemaal. Kennelijk discrimineert het schaakbord niet alleen op een zichtbare, maar ook nog op een onzichtbare manier tegen lopers.
Dat laatste betekent dus ook dat het niet mogelijk is om de mobiliteit van de toren en loper te gebruiken om de waarde van √2 te benaderen, wat ik eigenlijk wel jammer vind.


Dan koploper Landa. Die kwam een goed kwartier te laat de speelzaal binnen, waar Robin Swinkels al zat te wachten. De tijdsachterstand zat Landa niet zichtbaar dwars. De stelling op zet 21 kwalificeerde de Rus als een 2 results position: winst voor hem of remise. Greenfeld die bij de analyse was, sprak van een 1,5 results-position: remise achtte hij veel waarschijnlijker dan winst voor wit. Swinkels had er zijn ideeen over: in de partij offerde hij dame tegen toren en loper, wat een onneembare stelling opleverde: remise. Hij had goed gespeeld, vond hij, maar wil onderhand wel graag het eerste volle punt scoren. Het halfje maakt de strijd om de eerste plaats spannender. Fridman is langszij gekomen: met 3,5 uit 4 delen Landa en hij nu de koppositie.
Hoi Alexandra, ik zie dat je een stuk tekst uit het verslag van de 3e HMC Calder Cup 2014 hebt gekopieerd. Dat toernooi kende ik niet, maar het ziet er wel interessant uit. Was je daarbij?